인공지능 1
Machine Learning
- Limitations of explicit programming (명시적 프로그래밍의 한계)
- Spam filter : many rules
- Automatic driving: too many rules
Machine Learning
: Field of study that gives computers the ability to learn without being explicitlt programmed.
-> 학습 능력을 갖는 프로그램
Superviesed/Unsupervised learning
Supervised
정해져있는 데이터. labeled examples - training set
ex) cat, dog, mug, hat 등의 label이 달려있는
Unsupervised learning : un-labeled data
Google news grouping
Word clustering
Supervised learing
- Most common problem type in ML
Image labeling : learning from tagged images
Email spam filter: learning from labeled (spam or ham) email
Predicting exam score : learning from previous exam score and time spent.
Traing data set
Supervised learning 의 예
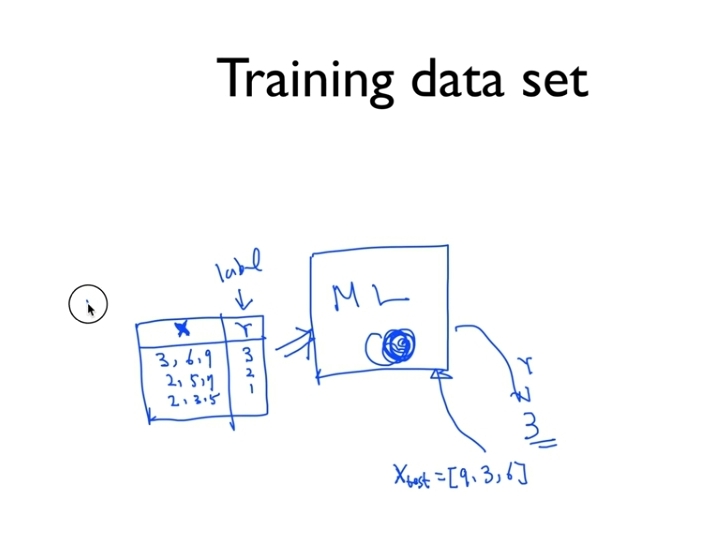
하나의 머신러닝이라는 모델이 있고, label을 보통 Y라고 함. X는 데이터.
label을 가지고 학습.
Xtest 라는 값을 모델에게 질문 하면 내가 생각하는 label(Y) 는 3이다. 이런식임.
AlphaGo
기존 사람들이 바둑을 둔 위치를 학습.
supervised learning 의 일종.
Types of supervised learning
- Predicting final exam score based on time spent : 공부한 시간에 따른 시험 성적 예측 시스템 0~100 -> regression
- Pass/non Pass 둘 중 하나. 분류. -> binary classification
- 공부한 시간에 따른 학점 예측 시스템. -> multi-label calssification.
| X(hours) | Y(Pass/Fail) |
| 10 | P |
| 9 | P |
| 3 | F |
| 2 | F |
binary classification
| x(hours) | y(scores) |
| 10 | 100 |
| 9 | 90 |
| 3 | 30 |
| 2 | 20 |
regression
| x(hours) | y(grade) |
| 10 | A |
| 9 | A |
| 3 | C |
| 2 | C |
multiple classification
Data Flow Graph
- Nodes in the graph represent mathematical operations
- Edges represent the multidimensional data arrays(tensors) communicated between them.
TensorFlow(텐서플로우)
- 가장 널리 쓰이는 딥러닝 프레임워크 중 하나
- 구글이 주도적으로 개발하는 플랫폼
- 파이썬, C++ API를 기본적으로 제공하고, 자바스크립트, 자바, 고, 스위프트 등 다양한 프로그래밍 언어를 지원
- tf.keras 를 중심으로 고수준 API 통합 (2.x 버전)
- TPU(Tensor Processing Unit) 지원 : 구글에서 자체적으로 만든 프로세싱 유닛
- TPU는 GPU보다 전력을 적게 소모, 경제적
- 일반적으로 32비트(float32)로 수행되는 곱셈 연산을 16비트(float16)로 낮춤
윈도우 설치
pip install --upgrade tensorflow
Hello Tensorflow! 실습

강의는 2016년거라 그런가 1.00 버전 텐서플로우를 써서 계속 오류가 발생함.
버전 2.0.0에서는 Session을 정의하고 run 해주는 과정이 생략된다고 함.

오류를 수정하면 Hello, Tensorflow가 올바르게 뜸.
Computational Graph
a와 b라는 노드를 더하기 노드로 연결
a = 3, b = 4라면 연결 시 7
Tensor = 그래프의 요소.
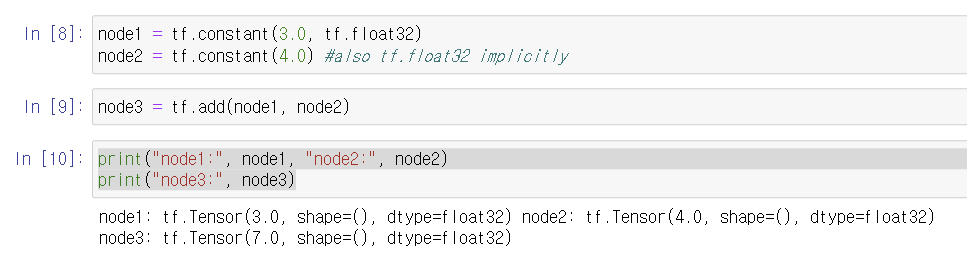
강의 예제에는 아래와 같이 해주어야 제대로 된 값이 출력되지만 버전 2는 안 해도 됨.
sess = tf.Session()
print("sess.run(node1, node2):", sess.run([node1, node2]))
print("sess.run(node3):", sess.run(node3))1. 그래프 build(설계)
2. 그래프 session run (버전 2.0.0부터는 no)
3. 그래프 출력
Placeholder
처음에 변수를 선언할 때 값을 바로 주는 것이 아니라, 나중에 값을 던져주는 공간을 만들어주는 것.

Tensorflow 2.0에서는 세션과 플레이스홀더를 사용하지 않고, @tf.function을 통해 함수를 정의함으로서 훨씬 간결하게 처리가 가능함.
간단한 사칙연산은 tensorflow 내장 연산자를 이용하면 훨씬 편함.
- tf.add : 덧셈
- tf.subtract : 뺄셈
- tf.multiply : 곱셈
- tf.divide : 나눗셈
- tf.pow : n제곱
- tf.negative : 음수 부호
- tf.abs : 절대값
- tf.sign : 부호
- tf.round : 반올림
- tf.math.ceil : 올림
- tf.floor : 내림
- tf.math.square : 제곱
- tf.math.sqrt : 제곱근
- tf.maximum : 두 텐서의 각 원소에서 최댓값만 반환
- tf.minimum : 두 텐서의 각 원소에서 최솟값만 반환
- tf. cumsum : 누적합
- tf.math.cumprod : 누적곱
Tensor Ranks, Shapes, and Types
1차원, 2차원, 3차원, .... , n차원
| Rank | Math entity | Python example |
| 0 | Scalar(magnitude only) | s = 483 |
| 1 | Vector(magnitude and direction) | v = [1.1, 2.2, 3.3] |
| 2 | Matrix(table of numbers) | m = [ [1,2,3], [4, 5, 6], [7, 8, 9] ] |
| 3 | 3-Tensor (cube of numbers) | t = [ [ [2], [4], [6] ], [ [8] , [10], [12] ] , [ [14], [16], [18] ] ] |
| n | n-Tensor (you get the idea) | .... |
각각의 element에 몇 개씩 들어있는지에 따라
| Rank | Shape | Dimension num | Python example |
| 0 | [] | 0-D | A 0-D tensor. A scalar. |
| 1 | [D0] | 1-D | A 1-D tensor with shape[5] |
| 2 | [D0, D1] | 2-D | A 2-D tensor with shape[3, 4] |
| 3 | [D0, D1, D2] | 3-D | A 3-D tensor with shape[1, 4, 3] |
| n | [D0, D1, ... Dn-1] | n-D | A tensor with shape [D0, D1, .... , Dn-1] |
Types
float32, int32 많이 사용
Linear Regression
Predicting exam score : regression -> Supervised Learning ( training데이터를 가지고 학습(training을 시킴)
0~100 사이 예측
| x(hours) | y(scores) |
| 10 | 90 |
| 9 | 80 |
| 3 | 50 |
| 2 | 30 |
| x | y |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
(Linear) Hyphothesis
선형 가설. 그래프 상에 일차함수로 나타나는 것들이 많음.
H(x) = Wx + b
그래프 상에 나타나는 일차함수(가설) 등 중 뭐가 더 좋은가. -> 실제 데이터와 가설 점들과의 거리 계산
Cost Function(Loss function)
How fit the line to our (training data)
(H(x) - y)^2
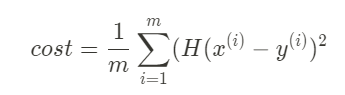
m = 데이터 갯수
이 공식의 값이 가장 작은 값을 갖게 하는 W, b 를 구하기 -> Linea regression의 학습
Goal : Minimize cost
x_train = [1, 2, 3]
y_train = [1, 2, 3]
W = tf.Variable(tf.random_normal([1]), name='weight')
b = tf.Variable(tf.random_normal([1]), name='bias')
hypothesis = x_train * W + b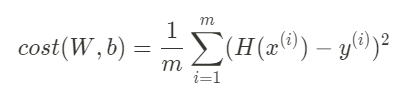
cost = tf.reduce_mean(tf.square(hypothesis - y_train))tf.reduce_mean 함수는 전체 평균을 내주는 역할.
GradiantDescent (경사 하강법)
- Minimize cost function
- Gradient descent is used many minimization problems.
- For a given cost function, cost(W, b), it will find W, b to minimize cost
딥러닝 알고리즘 학습 시 사용되는 최적화 방법 중 하나.
딥러닝 알고리즘 학습 시 목표는 예측값과 정답값 간의 차이인 손실 함수의 크기를 최소화시키는 파라미터를 찾는 것임.
학습 데이터 입력을 변경할 수 없기 때문에, 손실 함수 값의 변화에 따라 가중치(weight) 혹은 편향(bias)을 업데이트해야함.
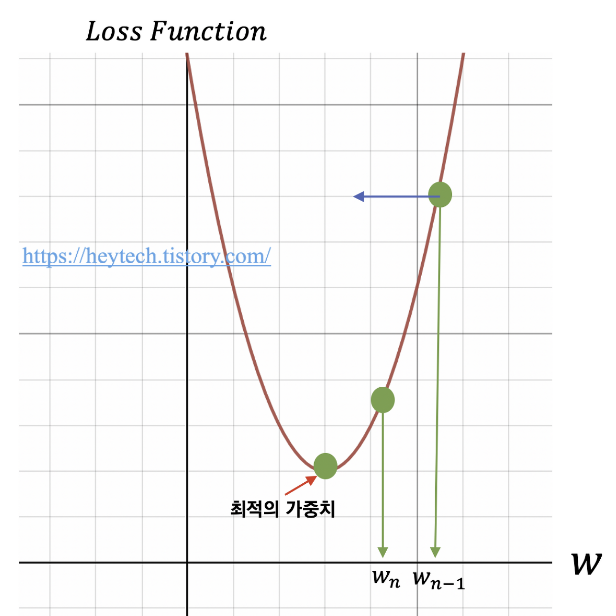
#Minimize
optimizer = tf.train.FradientDescentOprimizer(learning_rate=0.01)
train = optimizer.minimize(cost)기울기 (-) : W가 커짐.
기울기 (+) : W가 작아짐.
구현
Output when W= -3 -> W가 커짐
import tensorflow.compat.v1 as tf
tf.disable_v2_behavior()
x = [1,2,3]
y = [1,2,3]
W = tf.Variable(-3.0)
hypothesis = x*W
cost = tf.reduce_mean(tf.square(hypothesis - y))
optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.1)
train = optimizer.minimize(cost)
sess = tf.Session()
sess.run(tf.global_variables_initializer())
for step in range(100):
print(step, sess.run(W))
sess.run(train)

경사하강법의 두 가지 한계
1. Local Minimum 문제
경사하강법은 비볼록 함수의 경우, 파라미터의 초기 시작 위치에 따라 최적의 값이 달라짐.
볼록함수는 어디서 출발하든 가운데로 모임.
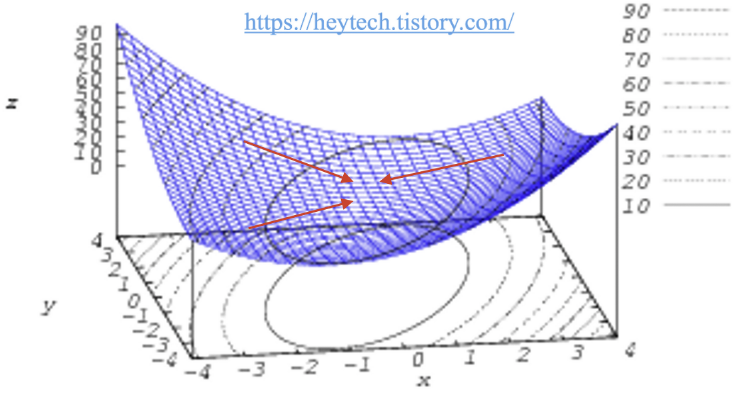
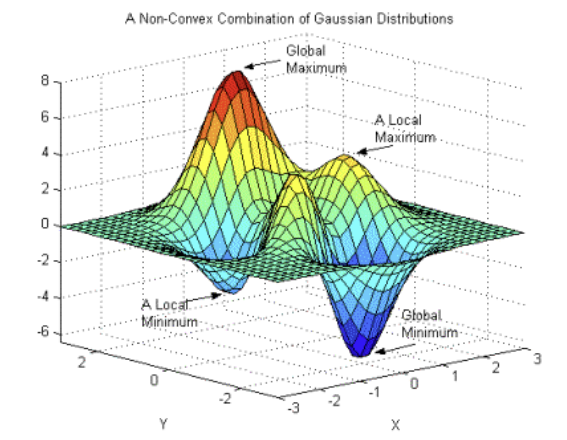
Local minimum = 그래프 내 일부만 고려했을 때의 최솟값.
경사 하강법으로 최적의 값인 줄 알았던 값이 Global minimum보다 큰 경우를 Local minimum이라고 할 수 있음.
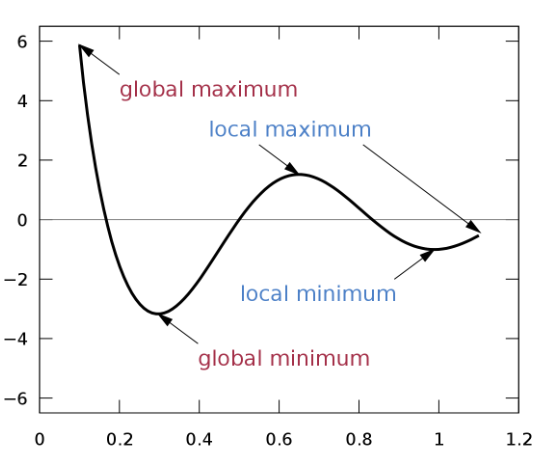
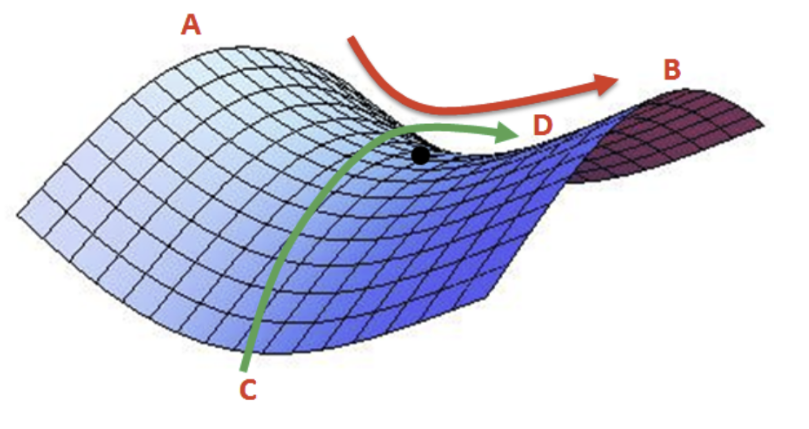
2. Saddle point 문제
A-B 사이에서 검은 점은 최솟값이지만, C-D 사이에서는 최댓값임. 따라서 해당 지점은 미분이 0이지만 극값을 가질 수 없음. 경사 하강법은 미분이 0일 경우 더이상 파라미터를 업데이트하지 않기 때문에, 이러한 안장점을 벗어나지 못하는 한계가 존재함.