인공지능 스터디 2
지난 시간 복습
Linear regression
- Hypothesis
- Cost function
- Gradient descent algorithm
Multivariable regression (다중 선형 회귀)
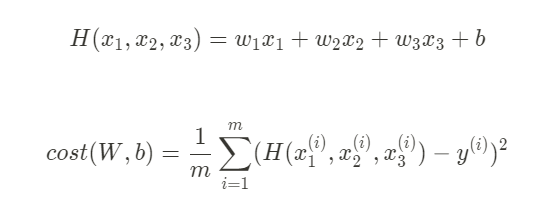
가설이 너무 복잡하니까 matrix(행렬의곱)를 사용해서 표현함.
입력 변수가 3개라면 weight도 3개가 됨.
H(X) = XW

5 = instance
입력 = 3, 출력 = 2
W = [입력, 출력]
WX vs XW
- theory
H(x) = Wx+b
- Implementation(Tensorflow)
H(X) = XW

TensorFlow로 파일에서 데이터 읽어오기

텍스트 파일을 주로 csv 파일로 저장하고 이를 불러옴.

파이썬에서 사용하는 슬라이싱을 통해 x와 y의 데이터를 나눔.

b[1,1]에서 앞의 1은 첫 번째 row를 말함. 그리고 뒤의 1을 통해 첫 번째 인자를 가져오게 됨.
데이터 파일에 있는 숫자들 중 앞의 3개는 x 데이터, 맨 마지막 숫자는 y데이터로 가져옴.

Queue Runners
특정 데이터를 불러와서 적당한 처리를 통해 우리가 필요한 데이터만 그때그때 메모리에 올려서 사용하는 구조.

1. 우리가 불러올 여러 개의 데이터 파일(파일들의 리스트)을 모두 적어줌으로서 queue에 올림.
2. 파일을 읽은 reader를 설정해줌.
3. 불러오는 값(value)을 어떻게 parsing 할 것인가를 설정함.

batch : 일종의 펌프 역할. 데이터를 읽어올 수 있도록 해주는 것.
데이터를 어떻게 읽어올 것인지 슬라이싱하여 설정함.
batch_size : 한번에 몇개를 가져올지 설정
Logistic Classification
classificaion 알고리즘 중 정확도가 높은 알고리즘.
- 실제 문제에도 적용 가능
- neural network과 딥러닝의 중요한 구성요소
Linear Regression 복습

Cost function : 가설과 실제 값의 차이를 평균낸 것
Gradient decent : 경사하강 알고리즘
기울기 = cost 함수를 미분한 값
알파 값 = 한 번에 움직이는 step size = learning rate
(Binary) Classfication
어떤 기준에 의해 데이터를 처리하고 이를 A인지 B인지 내지는 1인지 0인지 식의 결과값을 얻고 싶을 때 사용함.
- Binary : 이분법적으로 분류.
- Multiple : 2가지 이상으로 분류.
- Spam Detection : Spam(0) or Ham(1)
- Facebook feed : show or hide
- Credit card Fraudulent transaction detection : legimate or fraud
-> 분실된 신용카드 이전에 쓰던 소비패턴을 ㅎ삭습하여 가짜를 판별
encoding Flase = 0 or True = 1 --> 기계적인 학습을 위하여 0,1로 encoding
- 예시
1. Radiology
이미지를 보고 이것이 악성 tumor(종양)인지 아닌지

Tumor size가 일정수준 0.5 이상으로 넘어가면 악성 종양이라고 판단하는 dataset.
사이즈가 엄청나게 큰 종양이 데이터에 들어왔다고 하면, 이때 linear regression을 classification에 적용했을 때 문제점이 나타남.
-> 데이터의 범위가 넓어짐. Linear Regression에서 가설함수인 직선은 데이터를 반영하여 기울어지게 됨. 우리가 악성 종양을 판단하던 기준점이 0.5가 아닌 그 이상의 큰 값이 됨.
기준점이 바뀌면 기존에 악성 종양으로 판단되어야 했던 것들이 정상으로 판단되는 문제가 발생함.
2. Finance
이 주식을 살 것인지 팔 것인지 이전 시장 동향을 학습하여 판단. 사람보다 더 잘하는 분야임.
Pass(1)/Fail(0) based on studt hours by Linear Regression

모델의 문제점 1
50시간을 공부하면 linear regression에서는 큰 값이 나와야
하지만 이 모델에서는 1(pass)의 값만 가질 것
학습시키면 선이 기울어질 것인데, 0.5와 비교했을 때 합격/불합격 기준선이 달라질 것임.
모델의 문제점 2
- We know Y is 0 or 1
- Hypothesis can give values large than 1 or less than 0
x=100이라면 x0.5 해서 50이라는 값이 나오는데, 이 값은 1을 훨씬 뛰어넘는 값임.
-> Linear regression이 간단하고 좋기는 하지만 0~1 사이의 값으로 함축할 수 있는 함수를 찾고싶음.
Logistic Hypothesis


Sigmoid : Curved in two directions, like the letter "S", or the Greek sigma
값이 커져도 1로 수렴하고 값이 작아져도 0으로 수렴하는 함수임.
z = wx
H(x) = g(z)

Logistic regression 의 cost 함수
sigmoid 함수로 cost 함수를 만들어보면, Logistic regression은 구불구불한 밥그릇 형태임.
새로운 H(x)는 linear하지 않기 때문에 시작점이 어디냐에 따라 평평한 곳을 만나면 해당 지점을 최저점이라고 잘못 인식하게됨. (Local minimum)
Global minimum을 찾는 것이 목표임.
로지스틱 회귀에서는 Gradient descent algorithm을 사용할 수 없음.

cost = 어떤 것의 합의 평균. 하나의 엘리먼트에 cost를 구해 평균내는 것.
c에 (H(x), y)를 넣어 y=1일 때, y=0일 때 두 가지로 나누어 함수를 정의함.
구부러진 함수의 원인 = 자연상수(e)의 지수.
-> 지수와 상극인 log 함수를 사용해서 Cost 함수를 평평하게 펴줌.

1. y(학습시킬 실제 데이터) = 1일 때
우리가 제대로 예측하여 H(x)=1 값을 갖는다치면
Cost 함수에 대한 결과가 매우 작은 값(거의 0)에 가깝게 나와서 cost가 작게 됨.
반대로 제대로 예측하지 못하여 H(x)=0 이 된다면 cost 함수의 결과는 거의 무한대에 가깝게 나와서 cost가 매우 크게 됨.
2. y=0
우리가 제대로 예측하여, H(x)=0일 때는 오른쪽 그래프에서 y=0이 됨. (cost=0)
1일 때는 오른쪽 그래프에서 y는 무한대가 됨. (cost = 무한대)
즉, 맞는 예측을 했을 때의 비용을 0으로 만들어줌으로서 cost 함수의 역할을 다하게 됨,

프로그래밍 시 편하게 할 수 있도록(if 문을 사용->굉장히 복잡해짐.) 수식을 조정한 것.

평평해진 Cost 함수로 Gradient descent algorithm을 사용할 수 있음.
Cost 함수의 기울기인 W를 구하기 위해 미분을 할 것임. 컴퓨터가 대신 미분(GradientDescent Optimizer())해줄거니까, 우리는 알파값만 적절히 주고 현재의 weight를 조금씩 업데이트 시키면 됨.
Multinomial
Multunimial classification 이란?

가설을 단순히 H(x)=WX라는 식으로 세운다면 결과값이 0 또는 1이 아닌 값이 나올 수 있기 때문에
z = H(x), g(x)= sigmoid 함수로 둬서 0과 1내의 값으로 결과가 나오도록 함.

단순히 0 또는 1로써 구별하는 것을 넘어, 다양한 것으로 분류하는 것.

위 그래프는 A, B, C 세 개의 종류로 구별하는 그래프임.
Logistic Regression 여러 개를 이용한다면 이러한 구현이 가능함.



3개의 식을 독립적으로 계산하는 것은 복잡하기 때문에
하나의 행렬 곱셈식으로 합쳐서 이용함.
Where is sigmoid?

X를 주게되면 0, 1로 나오지 않고 vector로 나올 것임.
빨간색처럼 실수값이 나오는 것이 아니라 0~1 사이의 값이 나오기 ㄹ원함.

- logistic classifier를 이용하여 벡터를 주어 계산을 하게 되면 y와 같은 입력 값에 대한 세 개의 vector 값이 나오게 됨.
- p의 값을 모두 더하면 1이 되는 형태로 표현하기 위한 것이 softmax임.
Softmax 함수

n개의 값을 softmax에 넣게 되면 값이 산출됨.
1. 0~1 사이의 값
2. 전체의 합이 1이 됨. -> 각각을 확률로 볼 수 있음.

'ONE-HOT ENCODING 기법'
이들 중 하나를 고를 수 있는 기법
제일 큰 값을 1로 두고 나머지를 0으로 둠.
argmax 이용(tensorflow)
Cost function
- CROSS-ENTROPY cost function

L : 실제 값
S(Y) (= Y의 hat. softmax 함수에 넣은 값.) : 예측 값
-> 이 둘 사이의 차이를 알기 위하여 CROSS-ENTROPY 함수를 통하여 구함.
예측이 맞은 경우에는 cost가 최소화(=0)되어야 함.
예측이 틀린 경우 최종값 = 무한대 --> 에측이 틀렸을 때 cost가 큰 값이 나와야 함.
Logistic cost vs Cross entropy

많은 형태의 training data가 있을 경우 : 전체의 거리를 (D) 구한 후 합하여 개수 나눔.

Loss(cost) function은 밥그릇 모양.
어디서 시작하든 경사면을 타고 내려가면 최저값을 찾을 수 있음.
경사면(기울기) = 함수를 미분하는 것.
알파값만큼 한 발자국씩 내려가면서 최저값을 찾게 됨.
x_data = [[1, 2, 1, 1], [2, 1, 3, 2], [3, 1, 3, 4], [4, 1, 5, 5], [1, 7, 5, 5],
[1, 2, 5, 6], [1, 6, 6, 6], [1, 7, 7, 7]]
y_data = [[0, 0, 1], [0, 0, 1], [0, 0, 1], [0, 1, 0], [0, 1, 0], [0, 1, 0], [1, 0, 0], [1, 0, 0]]
# y value가 여러개의 class가 있으므로 one hot encoding을 이용해 표현했다. 2,2,2,1,1,1,0,0
X = tf.placeholder("float", [None, 4])
Y = tf.placeholder("float", [None, 3])
nb_classes = 3
W = tf.Variable(tf.random_normal([4, nb_classes]), name='weight')
b = tf.Variable(tf.random_normal([nb_classes]), name='bias')
# tf.nn.softmax computes softmax activations
# softmax = exp(logits) / reduce_sum(exp(logits), dim)
hypothesis = tf.nn.softmax(tf.matmul(X,W) + b)
# Cross entropy cost/loss
cost = tf.reduce_mean(-tf.reduce_sum(Y * tf.log(hypothesis), axis=1))
optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.1).minimize(cost)
# Launch graph
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for step in range(2001):
sess.run(optimizer, feed_dict={X: x_data, Y: y_data})
if step % 200 == 0:
print(step, sess.run(cost, feed_dict={X: x_data, Y: y_data}))
WARNING:tensorflow:From C:\Users\whanh\AppData\Local\Continuum\anaconda3\lib\site-packages\tensorflow\python\framework\op_def_library.py:263: colocate_with (from tensorflow.python.framework.ops) is deprecated and will be removed in a future version.
Instructions for updating:
Colocations handled automatically by placer.
WARNING:tensorflow:From C:\Users\whanh\AppData\Local\Continuum\anaconda3\lib\site-packages\tensorflow\python\ops\math_ops.py:3066: to_int32 (from tensorflow.python.ops.math_ops) is deprecated and will be removed in a future version.
Instructions for updating:
Use tf.cast instead.
0 5.5452747
200 0.591108
400 0.49374837
600 0.40227863
800 0.31145102
1000 0.23698442
1200 0.21411678
1400 0.19557284
1600 0.17987308
1800 0.16642055
2000 0.15477483Fancy Softmax 구현

