AES(Advanced Encryption Standard)
연산 능력 향상으로 DES가 안전하지 않게 된 것에 대한 대안.
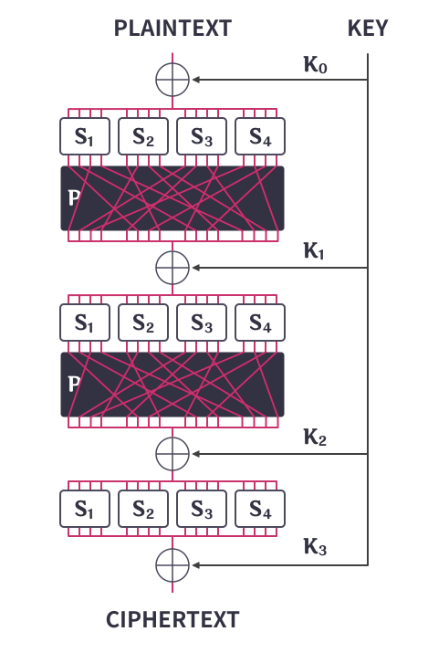
SPN(Substitution Permutation Network) 암호 구조
- 곱 암호의 일종.
치환(Substitution) - S-Box 사용
순열(Permutation) - P-Box 사용
여러 라운드에 걸쳐 반복함.
페이스텔 구조와 달리 라운드마다 입력 전체에 라운드 함수를 적용하므로 같은 수의 라운드를 사용할 때 두 배의 암호학적 안전성을 갖는다.
AES 구조
라운드마다 128비트 크기의 블록을 암호화하는 블록 암호.
키 길이 = 128, 192,256 비트 중 하나 선택
라운드 수 = 키 길이에 따라 10, 12, 14
* AES-128 = 키 길이 128비트
1. 각 블록 4행 4열 상태 배열(State) 재구성.
각 칸에는 8비트(1바이트) 저장됨.
1F3CF203B211C5AA6EB27A45E4D98130의 State

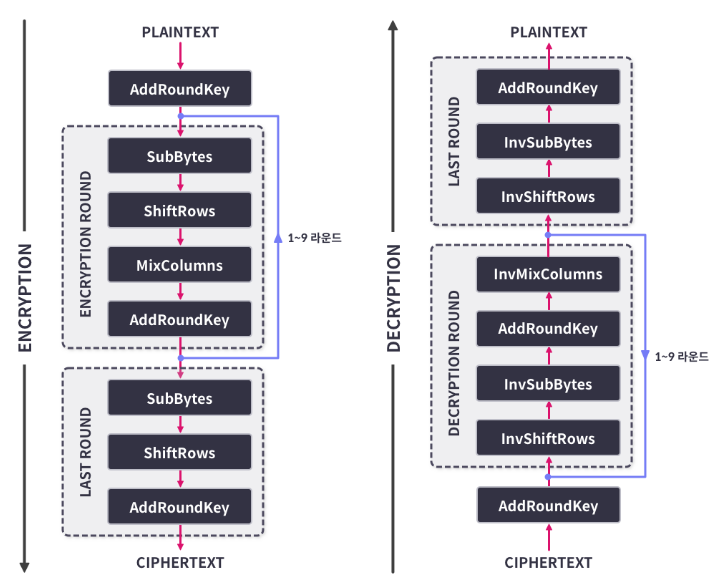
2. 재구성된 입력에 대해 AddRoundKey 함수 적용.
3. 마지막 라운드 전까지 매 라운드마다 SubBytes, ShiftRows, MixColumns, AddRoundKey 함수 반복 적용
4. 마지막 라운드에서는 MixColumns 제외
이 함수들에는 역함수가 존재함. -> 복호화가 역함수를 이용하여 이뤄짐.
AES 라운드 함수
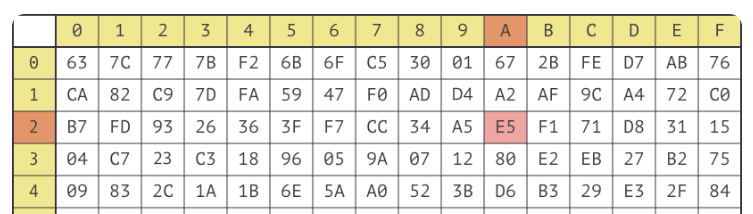
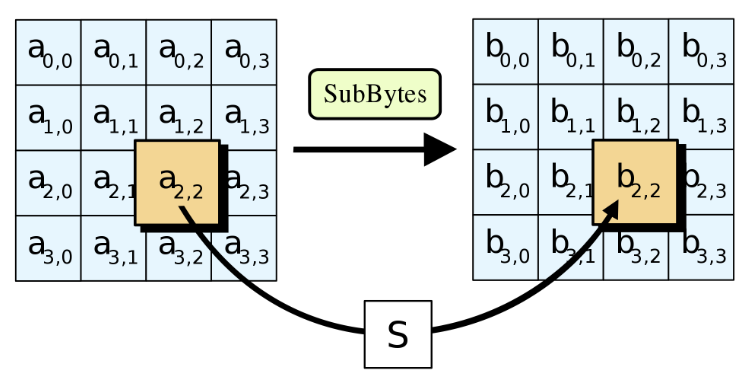
1. SubBytes
State의 각 바이트를 S-Box 참조하여 치환하는 함수.
상위 4비트가 행, 하위 4비트가 열을 결정.
어떤 바이트가 2A라면 2행 A열을 S-Box에서 참조하여 치환함.
2. ShiftRows
State의 각 행을 구성하는 바이트들을 쉬프트하는 함수.
4가지 함수 중 유일한 순열 역할.

위를 보면 2행은 왼쪽으로 1칸, 3행은 왼쪽 2칸, 4행은 왼쪽으로 3칸을 밀었음.
복호화는 각각 움직인 칸 수 만큼 반대로 밈.

3. MixColumns
열 단위 치환 수행 함수.
갈루아 필드 내에서의 행렬 연산으로 구해짐.

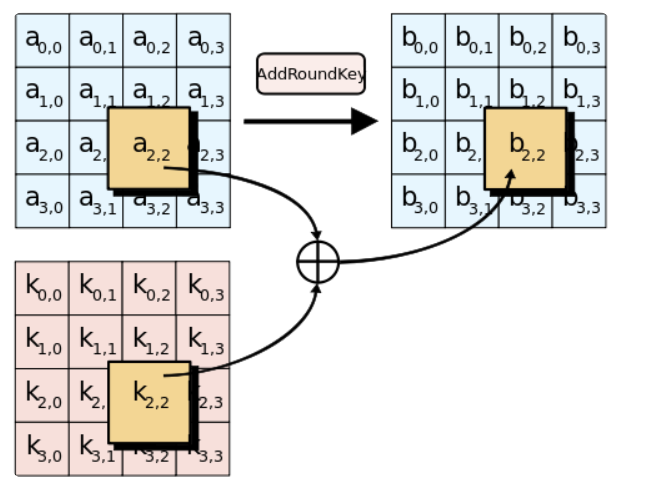
4. AddRoundKey
키 생성 함수(Key Schedule)
생성된 라운드 키의 state를 각 바이트별로 XOR함.
복호화 시에는 XOR의 성질을 이용하여 동일한 키를 state에 XOR함.
Key Schedule
키 생성 함수 : 입력된 키로부터 각 라운드에 쓰일 라운드 키 생성.
AES-128

aes는 암복호화 시작과 매라운드마다 AddRoundKey를 적용함.
AES-128에서는 라운드 키가 11개 필요.
각 라운드 키는 4행 4열 이니까 총 4행 44열의 키 행렬을 만들고, 이를 4열 씩 나눠서 매 AddRoundKey마다 사용
첫번째 AddRoundKey = 입력된 키 그대로 사용.
W0, W1, W2, W3 = 입력된 키의 각 열들과 같음.
W i>=4 생성 : W i-1 RotWord, SubWord, Rcon 적용 -> W i-4와 XOR하여 생성.
W4 생성 과정
일단 W3에 RotWord, SubWord, Rcon 적용함.
1. RotWord
열을 위쪽 방향으로 한 칸 씩 이동시켜서 한 번 회전하도록 함.

2. SubWord
SubBytes가 사용한 것과 동일한 S-Box 사용하여 각 바이트를 치환.
C행 F열, 4행 F열, 이런 식으로.
3. Rcon
R = [01, 02, 04, 08, 10, 20, 40, 80, 1B, 36]
Wi의 최상위 바이트를 R[i/4 - 1]과 XOR함.

W0과 Rcon의 출력을 XOR하면 됨.

세 가지 과정을 반복하여 W43까지 생성하고, 4열씩 각 라운드에 사용함.
W0 ~ W3은 시작 시 사용했으니 1라운드에서는 W4 ~W7이 사용됨.
Rcon, 그리고 열과 기존의 열을 XOR하는 과정은 키의 길이에 따라 조금 차이가 있다고 함.
DES

치환 - 혼돈 성질
순열 - 확산 성질
단순한 두 연산을 여러 번 교차해서 반복하면 혼돈과 확산의 성질을 만족함.
곱 암호(Product Cipher) : 단순한 연산들로 구성된 각 라운드를 여러 번 반복하는 암호.
페이스텔 구조(Feistel)
DES 라운드 함수 적용 전체 과정

(1) 입력으로 들어온 블록을 동일한 길이의 왼쪽 블록 L과 오른쪽 블록 R로 나눔.
(2) 각 라운드마다 오른쪽 블록은 다음 라운드의 왼쪽 블록이 됨.
(3) 왼쪽 블록은 오른쪽 블록에 라운드 함수 F를 적용한 결과와 xor 되어 다음 라운드의 오른쪽 블록으로 입력됨.
P = 입력으로 들어온 평문
K = 각 라운드에서 생성된 키.
특징
복호화 과정에서 F가 로 상쇄되므로 역함수가 존재하지 않아도됨.
암호화와 복호화구조가 동일함, 라운드 키를 역순으로 입력하면 복호화가 이뤄짐.
안전성을 갖기 위해 두 배 정도 라운드를 사용해야 함.

시작 : 초기 순열(Initial Permutation, IP)
마지막 : 최종 순열(Final Permutation, FP)
정해진 테이블(IPT, FTP)이용. 64비트 입력을 비트 단위로 전치함.
테이블의 n번째 값이 m일 때, 출력의 n 번째 비트는 입력의 m번째 비트가 됨.
두 순열은 서로 역관계.
임의의 64비트 데이터에 초기 순열을 적용하고 최종 순열을 적용하면 입력 값이 그대로 출력됨.
안전성 증가 x, DES를 하드웨어에 구현하기 쉽게함.
#!/usr/bin/python3
# Name: des.py
# Initial/Final Permutation Table
IPT = [58, 50, 42, 34, 26, 18, 10, 2,
60, 52, 44, 36, 28, 20, 12, 4,
62, 54, 46, 38, 30, 22, 14, 6,
64, 56, 48, 40, 32, 24, 16, 8,
57, 49, 41, 33, 25, 17, 9, 1,
59, 51, 43, 35, 27, 19, 11, 3,
61, 53, 45, 37, 29, 21, 13, 5,
63, 55, 47, 39, 31, 23, 15, 7]
FPT = [40, 8, 48, 16, 56, 24, 64, 32,
39, 7, 47, 15, 55, 23, 63, 31,
38, 6, 46, 14, 54, 22, 62, 30,
37, 5, 45, 13, 53, 21, 61, 29,
36, 4, 44, 12, 52, 20, 60, 28,
35, 3, 43, 11, 51, 19, 59, 27,
34, 2, 42, 10, 50, 18, 58, 26,
33, 1, 41, 9, 49, 17, 57, 25]
def plain2bitstring(plain: str):
return "".join(format(ord(c), "0>8b") for c in plain)
def plain2bitarray(plain: str):
bitstring = plain2bitstring(plain)
encoded = bytearray([int(b) for b in bitstring])
return encoded
def bitarray2plain(bitarray: bytearray):
bitstring = bitarray2bitstring(bitarray)
encoded = "".join([chr(int(bitstring[i*8:i*8+8], 2))
for i in range(len(bitstring)//8)])
return encoded
def bitarray2bitstring(bitarray: bytearray):
return "".join([str(b) for b in bitarray])
def permutation(block: bytearray, table: list[int], outlen: int):
permutated = bytearray(outlen)
for n in range(len(table)):
m = table[n]-1
permutated[n] = block[m]
return permutated
plain = "DEScrypt"
key = "DREAMCRY"
bitarray = plain2bitarray(plain)
print(f"bitstring of '{plain}': {bitarray2bitstring(bitarray)}")
# Initial permutation
initial_permutated = permutation(bitarray, IPT, 64)
print(
f"bitstring of initial_permutated: {bitarray2bitstring(initial_permutated)}")
# Final permutation
final_permutated = permutation(initial_permutated, FPT, 64)
print(f"bitstring of final_permutated: {bitarray2bitstring(final_permutated)}")
# plain == FP(IP(plain)) => FP = IP^{-1}
print(f"plaintext of final_permutated: {bitarray2plain(final_permutated)}")
라운드 함수
F에는 오른쪽 블록만 입력. 입력 길이는 32비트.
확장 순열(Expansion P-Box), 라운드 키 결합(XOR), 치환 테이블(S-Box), 고정 순열(Straight P-Box)

확장 순열과 라운드 키 결합
입력을 비트 단위로 전치하는 동시에, 전체 길이를 48비트로 확장함.
32비트를 4비트씩 8개의 부분으로 나누고, 테이블을 참조하여 각각을 6비트로 확장함.
테이블만 다르고, 초기 순열, 최종 순열과 같은 방식으로 이뤄짐.
라운드 키 결합 : 확장 순열로 나온 출력을 라운드 키 K와 xor하는 것.

S-Box와 고정 순열
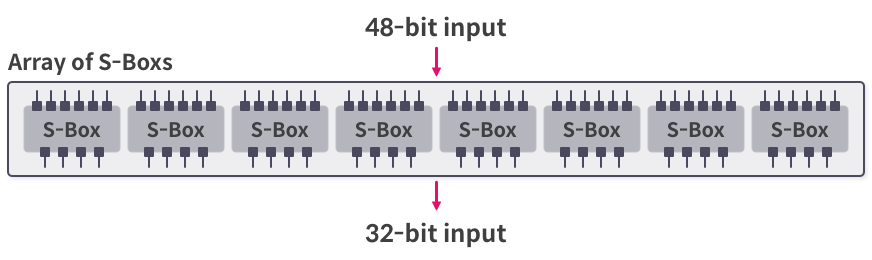
라운드 키 결합에서 출력된 48비트 결과 값을 32비트로 축소.
1. 입력을 여섯 비트 씩 8개
2. 여섯 비트 중 첫 번째와 마지막 비트로 행 결정, 나머지 네 개 비트로 열 결정.
3. S-Box에서 행과 열을 참조하여 값을 반환함.
DES에서는 자른 부분마다 다른 S-Box 사용.
길이 축소 이후 고정 순열로 다시 비트 단위 전치가 이뤄짐.
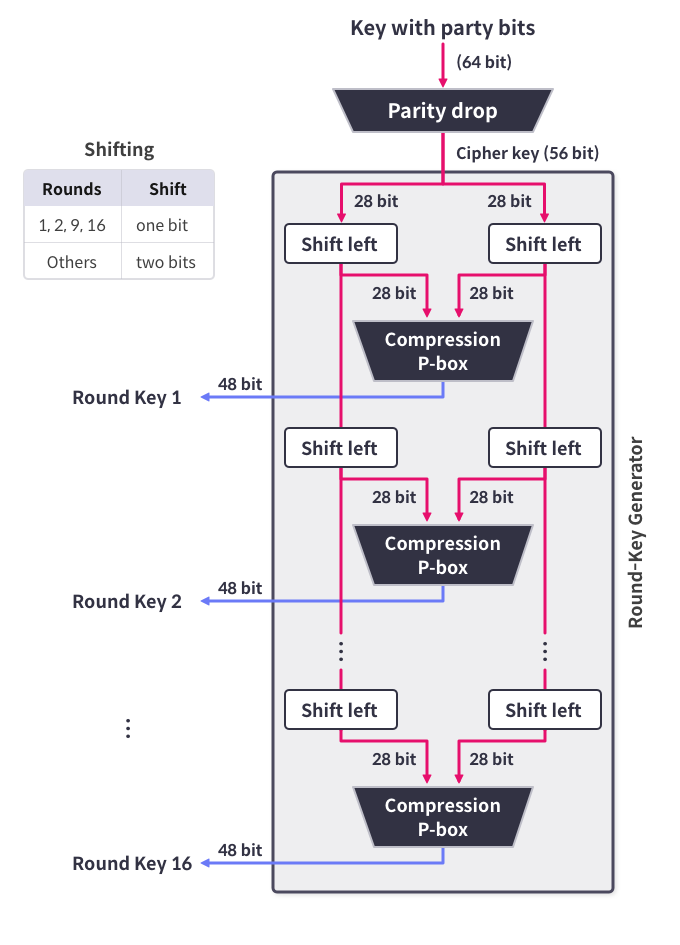
키 생성 함수
64비트 입력을 받아 각 라운드에 필요한 48비트 라운드 키 생성.
패리티 비트 제거(Parity Bit Drop)
입력에서 패리티 비트를 제거하고 남은 56비트에 순열을 적용함.
des 비밀키에서 각 바이트의 가장 오른쪽 비트는 자신이 속한 바이트의 나머지 7비트에 대한 홀수 패리티 비트(Odd Paity Bit) 임.
한 바이트를 이진수로 표현했을 때, 1읠 개수가 홀수가 되도록 덧붙인 비트.
-> 1이 4개 있으면 끝에 비트 1 덧붙이기
통신 중에 비트 반전이 일어나지 않았음을 보증.
수신한 바이트 중 1의 개수가 짝수인 바이트가 있다면 임의의 비트에 반전이 일어났음을 알 수 있고, 재전송 요구할 수 있음
쉬프트
입력 = 28(좌) + 28(우) 각각을 1비트나 2비트만큼 왼쪽으로 순환 쉬프트함.
1, 2, 9, 16 라운드에서는 1비트, 나머지는 2비트만큼 쉬프트함.
압축 순열
compression p-box
56비트 입력 -> 48비트 압축
앞서 말한 순열들과 같은 수행 방법.
DES 응용
1. 다중 DES
서로 다른 키를 사용하는 DES 모듈을 여러 개 이어 붙여서 약점 보완.
이중 = 2-DES 112비트
-> 단일과 안전성 별 차이 없음.
삼중 = 3-DES 168비트 키
-> 키 길이 두배 늘리는 정도

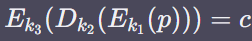
중간 일치 공격
어떤 평문 p와 암호문 c를 알 수 있을 떄 수행하는 공격.
- 56비트 키 공간 K에서 가능한 모든 키 k_1으로 p를 암호화하여 집합 S_1를 생성한다.
S_1 = \{E_{k_1}(p) | k_1\in K\} - K에서 가능한 모든 키 k_2로 c를 복호화하여 집합 S_2를 생성한다.
S_2 = \{D_{k_2}(c) | k_2\in K\} - S_1의 모든 원소와 S_2의 모든 원소에 대해 E_{k_1}(p) = D_{k_2}(c)를 만족하는 k_1, k_2의 쌍으로 후보키의 집합 CK를 생성한다.
CK=\{(k_1,k_2)|E_{k_1}(p)=D_{k_2}(c), E_{k_1}(p)\in S_1, D_{k_2}(c)\in S_2\} - 다른 평문 p'과 p'을 암호화한 암호문 c'을 생성한다.
- CK의 모든 원소에 대해 E_{k_1}(p')=D_{k_2}(c')을 만족하는 k_1과 k_2의 쌍으로 집합 CK를 갱신한다.
CK=\{(k_1,k_2)|E_{k_1}(p')=D_{k_2}(c'), (k_1, k_2) \in CK\} - CK의 원소가 하나가 될 때까지 4와 5의 과정을 반복한다.
-> 1, 2에서 2의 56승 번의 DES 암복호화 = 연산량에 유의미한 영향을 미침.
-> 3 후보키 생성 : 퀵정렬과 이분 탐색으로 빠르게 수행 가능.
-> 4, 5, 6 반복 횟수 많지 않음.
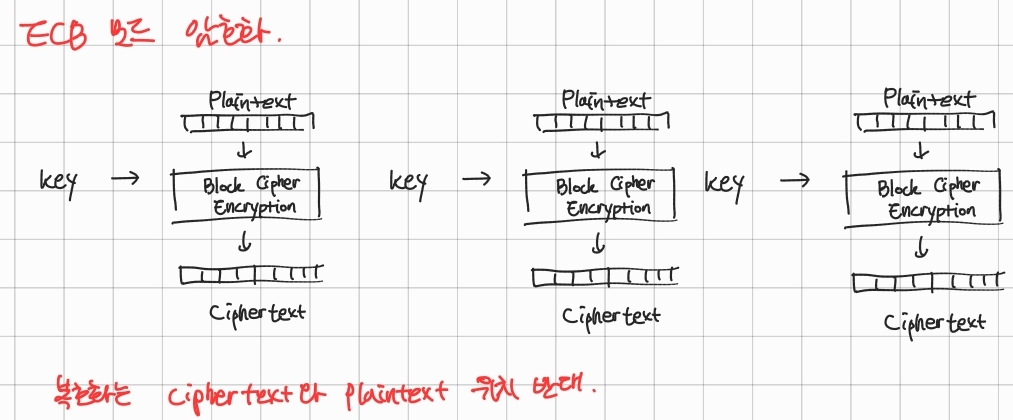
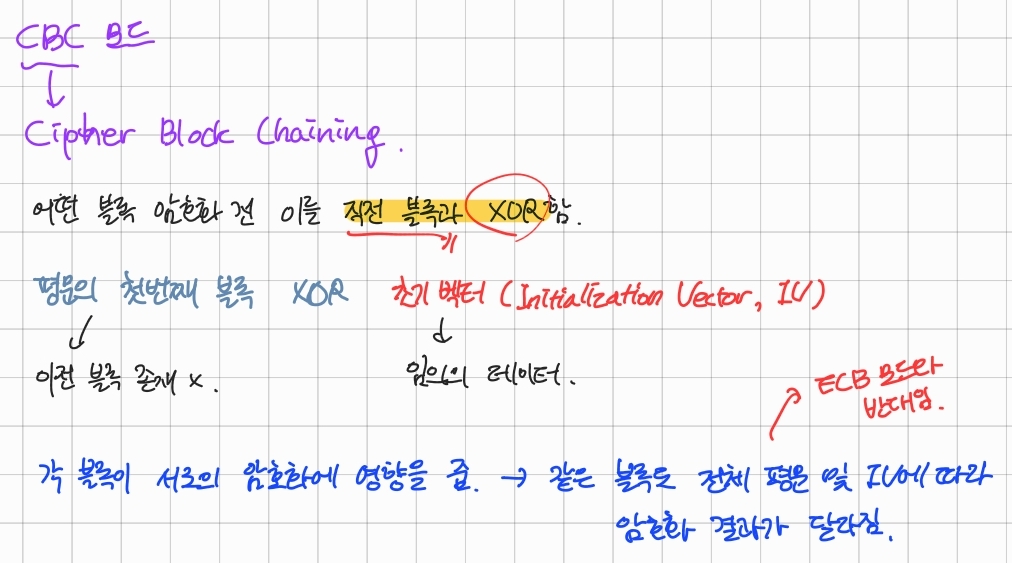
운영 모드












'Dreamhack' 카테고리의 다른 글
| CSRF 실습 (0) | 2022.08.05 |
|---|---|
| 암호학 Stage 4 (0) | 2022.08.05 |
| 암호학 Stage 2 (0) | 2022.07.30 |
| 암호학 Stage 1 (0) | 2022.07.30 |
| 웹 해킹 : XSS-2 (0) | 2022.07.25 |